Thuật toán tìm kiếm nhị phân (Binary Search) được sử dụng để tìm kiếm một giá trị trong một danh sách đã sắp xếp. Thuật toán này cài đặt theo phương pháp đệ quy sẽ giảm số phép toán so sánh và làm cho thuật toán chạy nhanh hơn. Trong trường hợp tệ nhất thì độ phức tạp của thuật toán sẽ là O(log n), với n là số phần tử của mảng.
Cách thực hiện
Ví dụ chúng ta có một mảng gồm các phần tử 1 2 4 6 7 8 9 10. Bây giờ chúng ta nhập vào một số nào đó. Ví dụ số cần tìm x=9, thuật toán sẽ làm như sau:
- Lấy giá trị chính giữa của dãy số y so sánh với x, nếu x nhỏ hơn thì tìm trong danh sách từ phần tử đầu tiên đến trước phần tử y, ngược lại thì tìm từ phần tử ngay sau y đến phần tử cuối cùng.
- Lặp lại bước trên cho đến khi gặp được x.
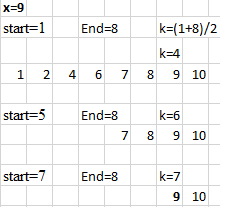
Đã tìm được x ở vị trí số 7.
Yêu cầu
Viết chương trình để cài đặt thuật toán tìm kiếm nhị phân (Binary Search) để tìm kiếm giá trị trong một mảng đã sắp xếp.
Phân tích và tìm cách giải
- Đầu vào: Một mảng số đã sắp xếp, giá trị x cần tìm.
- Đầu ra: In ra vị trí tìm được trong mảng
- Phân tích:
- – Hàm sử tìm kiếm BinarySearch(a[], start, end)
- – Tính k=(start + end)/2
- – Bước cơ sở:
- If a[k] = x -> return k //tìm thấy
- If k=end -> return -1 //không tìm thấy
- Bước đệ qui:
- If a[k] <x</li
- BinarySearch(a[], start, k-1)
- Else
- BinarySearch(a[], k+1, end)
Cách biểu diễn thuật toán tìm kiếm nhị phân (Binary Search)
Trong trường hợp này, tôi sử dụng ngôn ngữ giả.
Declare int a[] ={1, 2, 4, 6, 7, 8, 9, 10}
Input x
Binary(a[],x,start,end){
Int k = (start + end)/2
If a[k]=x then return k //Tìm thấy tại vị trí k
If k=end then return -1 // Không tìm thấy
If a[k]>x then
Binary(a[],x,start,k-1)
Else
Binary(a[],x,k+1,end)
}
Trên đây là một số thuật toán cơ bản, hay gặp nhằm giúp các bạn mới học thuật toán dễ dàng tiếp cận. Trong thời gian tới tôi sẽ tiếp tục cập nhật những thuật toán ở cấp độ khó hơn để các bạn có cơ hội rèn luyện sâu hơn.